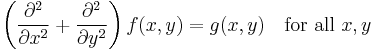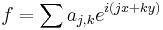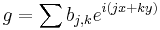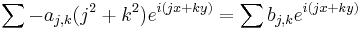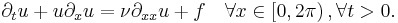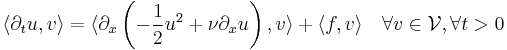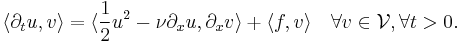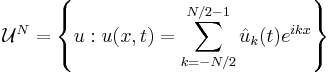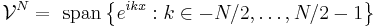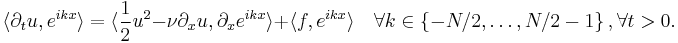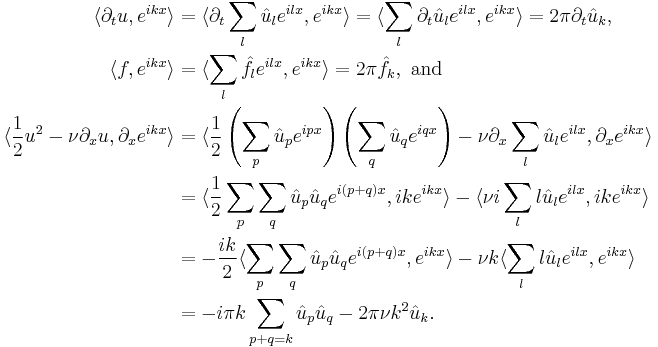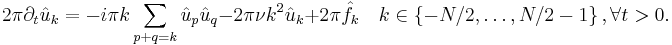Spectral method

Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain Dynamical Systems, often involving the use of the Fast Fourier Transform. Where applicable, spectral methods have excellent error properties, with the so called "exponential convergence" being the fastest possible. Spectral methods were developed in a long series of papers by Steven Orszag starting in 1969 including, but not limited to, Fourier series methods for periodic geometry problems, polynomial spectral methods for finite and unbounded geometry problems, pseudospectral methods for highly nonlinear problems, and spectral iteration methods for fast solution of steady state problems.

Partial differential equations (PDEs) describe a wide array of physical processes such as heat conduction, fluid flow, and sound propagation. In many such equations, there are underlying "basic waves" that can be used to give efficient algorithms for computing solutions to these PDEs. In a typical case, spectral methods take advantage of this fact by writing the solution as its Fourier series, substituting this series into the PDE to get a system of ordinary differential equations (ODEs) in the time-dependent coefficients of the trigonometric terms in the series (written in complex exponential form), and using a time-stepping method to solve those ODEs.

The spectral method and the finite element method are closely related and built on the same ideas; the main difference between them is that the spectral method approximates the solution as linear combination of continuous functions that are generally nonzero over the domain of solution (usually sinusoids or Chebyshev polynomials), while the finite element method approximates the solution as a linear combination of piecewise functions that are nonzero on small subdomains. Because of this, the spectral method takes on a global approach while the finite element method is a local approach. This is part of why the spectral method works best when the solution is smooth. In fact there are no known three-dimensional single domain spectral shock capturing results.[1]

In the finite element community, a method where the degree of the elements is very high or increases as the grid parameter h decreases to zero is sometimes called a spectral element method.

The implementation of the spectral method is normally accomplished either with collocation or a Galerkin or a Tau approach.

Contents

Examples of spectral methods

A concrete, linear example

Here we presume an understanding of basic multivariate calculus and Fourier series. If g(x,y) is a known, complex-valued function of two real variables, and g is periodic in x and y (that is, g(x,y)=g(x+2π,y)=g(x,y+2π)) then we are interested in finding a function f(x,y) so that

\left(\frac{\partial^2}{\partial x^2}%2B\frac{\partial^2}{\partial y^2}\right)f(x,y)=g(x,y)\quad \text{for all } x,y

where the expression on the left denotes the second partial derivatives of f in x and y, respectively. This is the Poisson equation, and can be physically interpreted as some sort of heat conduction problem.

If we write f and g in Fourier series:

f=\sum a_{j,k}e^{i(jx%2Bky)}
g=\sum b_{j,k}e^{i(jx%2Bky)}

and substitute into the differential equation, we obtain this equation:

\sum -a_{j,k}(j^2%2Bk^2)e^{i(jx%2Bky)}=\sum b_{j,k}e^{i(jx%2Bky)}

We have exchanged partial differentiation with an infinite sum, which is legitimate if we assume for instance that f has a continuous second derivative. By the uniqueness theorem for Fourier expansions, we must then equate the Fourier coefficients term by term, giving

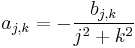
(*) a_{j,k}=-\frac{b_{j,k}}{j^2%2Bk^2}

which is an explicit formula for the Fourier coefficients aj,k.

With periodic boundary-conditions, the Poisson equation possesses a solution only if b0,0 = 0. Therefore we can freely choose a0,0 which will be equal to the mean of the resolution. This corresponds to choosing the integration constant.

To turn this into an algorithm, only finitely many frequencies are solved for. This introduces an error which can be shown to be proportional to 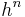h^n, where 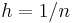h=1/n and n is the highest frequency treated.

Algorithm

  1. Compute the Fourier transform (bj,k) of g.
  2. Compute the Fourier transform (aj,k) of f via the formula (*) and the Fourier transform of g.
  3. Compute f by taking an inverse Fourier transform of (aj,k).

Since we're only interested in a finite window of frequencies (of size n, say) this can be done using a Fast Fourier Transform algorithm. Therefore, globally the algorithm runs in time O(n log n).

A concrete, nonlinear example

We wish to solve the forced, transient, nonlinear Burgers' equation using a spectral approach.

Given 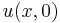u(x,0) on the periodic domain 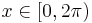x\in\left[0,2\pi\right), find 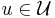u \in \mathcal{U} such that

\partial_{t} u %2B u \partial_{x} u = \nu \partial_{xx} u %2B f \quad \forall x\in\left[0,2\pi\right), \forall t>0.

In weak, conservative form this becomes

\langle \partial_{t} u , v \rangle = \langle \partial_x \left(-\frac{1}{2} u^2 %2B \nu \partial_{x} u\right) , v \rangle %2B \langle f, v \rangle \quad \forall v\in \mathcal{V}, \forall t>0

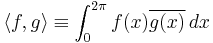where \langle f, g \rangle \equiv \int_{0}^{2\pi} f(x) \overline{g(x)}\,dx following inner product notation. Integrating by parts and using periodicity grants

\langle \partial_{t} u , v \rangle = \langle \frac{1}{2} u^2 - \nu \partial_{x} u , \partial_x v\rangle%2B\langle f, v \rangle \quad \forall v\in \mathcal{V}, \forall t>0.

To apply the Fourier−Galerkin method, choose both

\mathcal{U}^N = \left\{ u�: u(x,t)=\sum_{k=-N/2}^{N/2-1} \hat{u}_{k}(t) e^{i k x}\right\}

and

\mathcal{V}^N =\text{ span}\left\{ e^{i k x}�: k\in -N/2,\dots,N/2-1\right\}

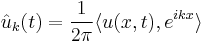where \hat{u}_k(t)=\frac{1}{2\pi}\langle u(x,t), e^{i k x} \rangle. This reduces the problem to finding 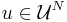u\in\mathcal{U}^N such that

\langle \partial_{t} u , e^{i k x} \rangle = \langle \frac{1}{2} u^2 - \nu \partial_{x} u , \partial_x e^{i k x} \rangle %2B \langle f, e^{i k x} \rangle \quad \forall k\in \left\{ -N/2,\dots,N/2-1 \right\}, \forall t>0.

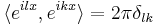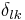Using the orthogonality relation \langle e^{i l x}, e^{i k x} \rangle = 2 \pi \delta_{lk} where \delta_{lk} is the Kronecker delta, we simplify the above three terms for each k to see

\begin{align} \langle \partial_{t} u , e^{i k x}\rangle &= \langle \partial_{t} \sum_{l} \hat{u}_{l} e^{i l x} , e^{i k x} \rangle = \langle \sum_{l} \partial_{t} \hat{u}_{l} e^{i l x} , e^{i k x} \rangle = 2 \pi \partial_t \hat{u}_k, \\ \langle f , e^{i k x} \rangle &= \langle \sum_{l} \hat{f}_{l} e^{i l x} , e^{i k x}\rangle= 2 \pi \hat{f}_k, \text{ and} \\ \langle \frac{1}{2} u^2 - \nu \partial_{x} u , \partial_x e^{i k x} \rangle &= \langle \frac{1}{2} \left(\sum_{p} \hat{u}_p e^{i p x}\right) \left(\sum_{q} \hat{u}_q e^{i q x}\right) - \nu \partial_x \sum_{l} \hat{u}_l e^{i l x} , \partial_x e^{i k x} \rangle \\ &= \langle \frac{1}{2} \sum_{p} \sum_{q} \hat{u}_p \hat{u}_q e^{i \left(p%2Bq\right) x} , i k e^{i k x} \rangle - \langle \nu i \sum_{l} l \hat{u}_l e^{i l x} , i k e^{i k x} \rangle \\ &= -\frac{i k}{2} \langle \sum_{p} \sum_{q} \hat{u}_p \hat{u}_q e^{i \left(p%2Bq\right) x} , e^{i k x} \rangle - \nu k \langle \sum_{l} l \hat{u}_l e^{i l x} , e^{i k x} \rangle \\ &= - i \pi k \sum_{p%2Bq=k} \hat{u}_p \hat{u}_q - 2\pi\nu{}k^2\hat{u}_k. \end{align}

Assemble the three terms for each k to obtain

2 \pi \partial_t \hat{u}_k = - i \pi k \sum_{p%2Bq=k} \hat{u}_p \hat{u}_q - 2\pi\nu{}k^2\hat{u}_k %2B 2 \pi \hat{f}_k \quad k\in\left\{ -N/2,\dots,N/2-1 \right\}, \forall t>0.

Dividing through by 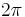2\pi, we finally arrive at

\partial_t \hat{u}_k = - \frac{i k}{2} \sum_{p%2Bq=k} \hat{u}_p \hat{u}_q - \nu{}k^2\hat{u}_k %2B \hat{f}_k \quad k\in\left\{ -N/2,\dots,N/2-1 \right\}, \forall t>0.

With Fourier transformed initial conditions 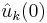\hat{u}_{k}(0) and forcing 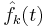\hat{f}_{k}(t), this coupled system of ordinary differential equations may be integrated in time (using, e.g., a Runge Kutta technique) to find a solution. The nonlinear term is a convolution, and there are several transform-based techniques for evaluating it efficiently. See the references by Boyd and Canuto et al. for more details.

A relationship with the spectral element method

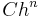One can show that if g is infinitely differentiable, then the numerical algorithm using Fast Fourier Transforms will converge faster than any polynomial in the grid size h. That is, for any n>0, there is a C<\infty such that the error is less than Ch^n for all sufficiently small values of h. We say that the spectral method is of order n, for every n>0.

Because a spectral element method is a finite element method of very high order, there is a similarity in the convergence properties. However, whereas the spectral method is based on the eigendecomposition of the particular boundary value problem, the spectral element method does not use that information and works for arbitrary elliptic boundary value problems.

See also

Finite difference methods
Finite volume methods
Finite element methods
Other methods
Domain decomposition methods

References

  1. ^ pp 235, Spectral Methods: evolution to complex geometries and applications to fluid dynamics, By Canuto, Hussaini, Quarteroni and Zang, Springer, 2007. .